Particle

The module enables the calculations of particle properties which currently include the calculations of surfaces and possible slip plane positions. All calculations relay on the usage of a crystal structure in order to calculate the requested properties.

Both analysis can be accessed by the following import:

>>> from ccdc import particle

Surface

The class ccdc.particle.Surface is used to generate slabs of atoms and molecules which represent particle surfaces, and to perform various analyses and descriptor calculations on those surfaces. The calculated surfaces store three information types: topological, atomistic and descriptor data. Topological information describes the “physical” surface with a mesh. The surfaces are generated as slabs containing atoms which possess positional and chemical data. Finally, a set of descriptors have been implemented to quantify the surface topology and chemistry.

Surfaces are constructed using the unit cell and its dimensions. The U and V vectors describe the boundaries required to represent a single repeat unit of a selected Miller indice. Figure 1 shows what U and V represent relative to the unit cell (U = a-axis , V = b-axis).

Figure 1. Surface unit cell diagram.

---

In order to calculate the particle surface, we first instantiate the Surface class with a crystal structure and a given hkl plane:

>>> from ccdc import io
>>> from ccdc.particle import Surface
>>> csd = io.EntryReader('CSD')
>>> hxacan = csd.crystal("HXACAN")
>>> hxacan_002 = Surface(hxacan, (0,0,2))

The surface object inherits the attributes of the ccdc.crystal class. Consequently, all crystal properties remain accessible.

>>> print(f"Crystal system : {hxacan_002.crystal.crystal_system}")
Crystal system : orthorhombic
>>> print(hxacan_002.crystal.cell_lengths)
CellLengths(a=11.805, b=17.164, c=7.393)

The slab, which is defined as the collection of atoms that make up the surface, can be accessed directly as either a single object or as a collection of molecules:

>>> slab = hxacan_002.slab
>>> print(f"Number of atoms in slab from Surface.slab           : {len(slab.atoms)}")
Number of atoms in slab from Surface.slab           : 240
>>> molecules = hxacan_002.slab_molecules
>>> atoms = [atom for molecule in molecules for atom in molecule.atoms]
>>> print(f"Number of atoms in slab from Surface.slab_molecules : {len(atoms)}")
Number of atoms in slab from Surface.slab_molecules : 240

It is also possible to access the list of molecules that make up the surface:

>>> molecules = hxacan_002.slab_molecules
>>> print(f"Number of molecules in slab : {len(molecules)}")
Number of molecules in slab : 12

Each individual molecule inherits attributes from the ccdc.molecule class:

>>> print(f"Chemical formula of first molecule : {molecules[0].formula}")
Chemical formula of first molecule : C8 H9 N1 O2
>>> print(f"Molecular weight of first molecule : {round(molecules[0].molecular_weight, 2)}")
Molecular weight of first molecule : 151.16

The topology (defined as the boundary generated by a probe of a given radius passing over the van der Waals radii of the slab atoms) can be accessed by two objects: triangles and nodes. Triangles are composed of three nodes. As such, instantiating the triangles list will return a mesh. Nodes describe the XYZ position of a single point of intersection. (Note - both triangles and nodes objects use generators to instantiate the data, so both require a constructor to access the data points)

>>> triangles = list(hxacan_002.topology.triangles)
>>> print(f"Number of triangles present in topology : {round(len(triangles), -3)}")
Number of triangles present in topology : 7000

The coordinates of each node in a triangle can be accessed individually or as a list:

>>> def format_node(n): return tuple(round(x,3) for x in n)
>>> def format_triangle(t): return tuple(format_node(n) for n in t)
>>> triangle = triangles[0]
>>> print(f"Accessing all nodes in triangle :\n{format_triangle(triangle)}")
Accessing all nodes in triangle :
((0.303, 0.0, 3.738), (0.303, 0.301, 3.722), (0.0, 0.0, 3.695))
>>> print(f"Accessing individual nodes :\n 1 : {format_node(triangle[0])}\n 2 : {format_node(triangle[1])}\n 3 : {format_node(triangle[2])}")
Accessing individual nodes :
 1 : (0.303, 0.0, 3.738)
 2 : (0.303, 0.301, 3.722)
 3 : (0.0, 0.0, 3.695)

Accessing all node positions (non-meshed) can be done as follows:

>>> nodes = list(hxacan_002.topology.nodes)
>>> print(f"Number of nodes in topology : {round(len(nodes),-3)}")
Number of nodes in topology : 4000

If you wish to return the atoms that exist “on the surface”, they can be accessed through the .surface_atoms attribute. Note - Atoms on the surface return those found in contact with nodes as defined by the overlapping vdW + grid_spacing used in the topology. Secondary Note - Atoms are from to the .slab Molecule object, as such any operations on these atoms or slab will propagate:

>>> surface_atoms = hxacan_002.surface_atoms
>>> print(f"Number of atoms in contact with the surface : {len(surface_atoms)}")
Number of atoms in contact with the surface : 64
>>> unique_atom_labels = { atom.label for atom in surface_atoms if atom.atomic_symbol != 'H'}
>>> print(f"Number of unique heavy atoms on surface : {len(unique_atom_labels)}")
Number of unique heavy atoms on surface : 11

All surface descriptors appear in the same sub-class:

>>> descriptors = hxacan_002.descriptors

The topology is described using four roughness measurements: rugosity, RMSD (Root mean squared deviation), skewness, and kurtosis.

The rugosity describes the ratio between the surface area and projected area. RMSD describes the deviation of nodes from the mean plane giving an idea of height deviations.

Figure 2. RMSD diagram.

Skewness calculates the degree of asymmetry of height values, indicating if a surface is dominated by peaks or valleys (around the mean plane). A negative skewness implies that the distribution is skewed towards the surface valleys.

Figure 3. Skewness diagram.

Kurtosis (Pearson) describes whether the height distribution is heavy-tailed or light-tailed around the mean plane. A normal distribution of height will have a kurtosis of 3. Heavy tailed data will have a kurtosis < 3 whilst those without tails will be > 3 .

Figure 4. Kurtosis diagram.

These descriptors can be accessed as follows:

>>> print(f"Rugosity : {descriptors.rugosity}")
Rugosity : 1.125
>>> print(f"RMSD : {descriptors.rmsd}\nSkewness : {descriptors.skewness}\nKurtosis : {descriptors.kurtosis}")
RMSD : 0.414
Skewness : 0.312
Kurtosis : 2.729

There are four chemical descriptors used to quantify the presence of hydrogen-bond (HB) donors, unsatisfied HB donors, HB acceptors, and aromatic bonds. The densities of (unsatisfied) HB donor/acceptor atoms and aromatic bonds are calculated by counting the number of relevant atoms in contact with the surface divided by the total projected area. Chemical descriptors can be accessed as follows:

>>> print(f"Density of HB-donors : {descriptors.hb_donors}")
Density of HB-donors : 0.039
>>> print(f"Density of Unsatisfied HB-donors : {descriptors.unsatisfied_hb_donors}")
Density of Unsatisfied HB-donors : 0.0
>>> print(f"Density of HB-acceptors: {descriptors.hb_acceptors}")
Density of HB-acceptors: 0.039
>>> print(f"Density of aromatic-bonds : {descriptors.aromatic_bonds}")
Density of aromatic-bonds : 0.118

The unsatisfied hb_donors are defined as hb_donors whose hydrogen atom is surface-terminating and not being used in an existing hydrogen bond. An example of the difference between hb_donors and unsatisfied_hb_donors can be seen in IBPRAC(002) in Figure 5.

>>> csd = io.EntryReader("CSD")
>>> ibprac = csd.crystal("IBPRAC")
>>> ibprac_surface = Surface(ibprac, miller_indices=(0,0,2))
>>> print(f"Density of HB-donors : {ibprac_surface.descriptors.hb_donors}")
Density of HB-donors : 0.026
>>> print(f"Density of Unsatisfied HB-donors : {ibprac_surface.descriptors.unsatisfied_hb_donors}")
Density of Unsatisfied HB-donors : 0.009

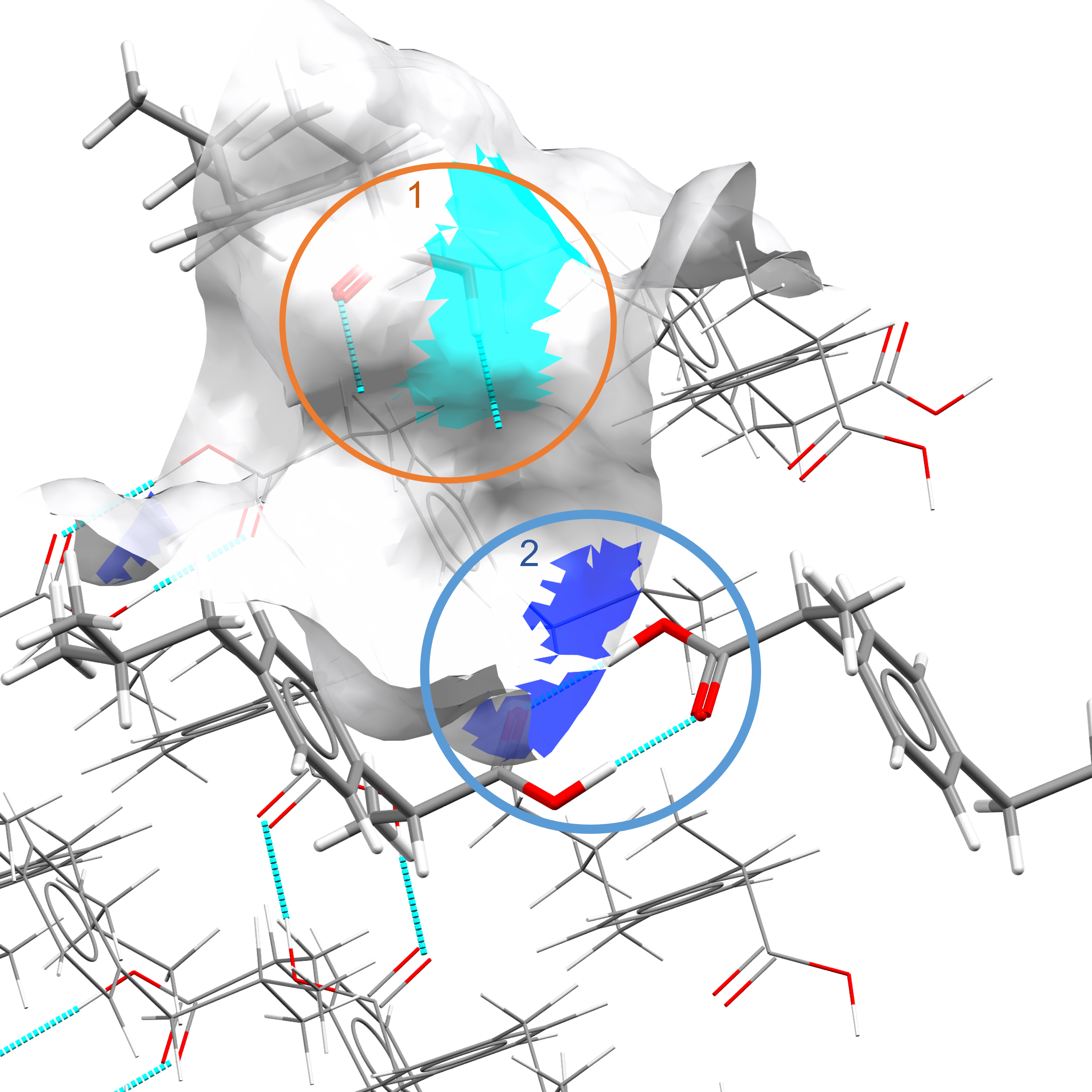
Figure 5. 1. Unsatisfied hydrogen bond donor. 2. Hydrogen bond donor.

Figure 5 illustrates the differences between hb_donors and unsatisfied_hb_donors. Circle 1 (unsatisfied_hb_donor) shows the carboxylic acid group surface-terminating with an incomplete hydrogen bond. Circle 2 (hb_donors) shows the same carboxylic acid group forming a dimer and thus the hydrogen atom is not available for further donation.

In order to account for differences in surfaces and systems, the Surface class has some advance options to enable analysis of more exotic surfaces, and the generation of larger slabs. Surface properties, such as thickness, plane offset, and the magnitude of the vectors U and V, can be modified to allow for changes in slab dimensions. The slab thickness is automatically calculated to be the cell diagonal distance from the unit cell origin to the opposite corner, but this can be modified by changing the thickness factor. Other optional parameters and their default values are offset=0.0, and surface_size = (1,1). These can be modified as follows:

>>> print(f"Surface area of 1x1x1.6 : {hxacan_002.descriptors.surface_area} A^2")
Surface area of 1x1x1.6 : 227.912 A^2
>>> larger_surface = Surface(hxacan,(0,0,2),surface_size=(2,2))
>>> print(f"Surface area of 2x2x1   : {larger_surface.descriptors.surface_area} A^2")
Surface area of 2x2x1   : 911.647 A^2
>>> offset_surface = Surface(hxacan, (0,0,2), offset=-2.0)
>>> print(f"Density of Aromatic bonds at -2.0 A surface offset: {offset_surface.descriptors.aromatic_bonds}")
Density of Aromatic bonds at -2.0 A surface offset: 0.128
>>> print(f"Density of Aromatic bonds at 0 A surface offset: {hxacan_002.descriptors.aromatic_bonds}")
Density of Aromatic bonds at 0 A surface offset: 0.118

The probe radius and grid spacing used to determine the surface topology can also be adjusted. In the case of most organic systems, default values of probe_radius = 1.2 and grid_spacing = 0.3 were found to be optimum to achieving smooth surfaces. By increasing the probe radius or grid spacing, the “resolution” of the surface is reduced and the number of nodes is decreased due to a reduction of sampling (grid spacing) and reduced possible contact (probe radius). It is however possible to access “smaller” pockets on the surface by reducing the probe radius.

>>> smoother_surface = Surface(hxacan, (0,0,2), probe_radius= 1.8, grid_spacing=0.5, thickness_factor=1.6)
>>> print(f"Smooth surface No. of nodes  : {len(list(smoother_surface.topology.nodes))}")
Smooth surface No. of nodes  : 1336
>>> print(f"Default surface No. of nodes : {len(list(hxacan_002.topology.nodes))}")
Default surface No. of nodes : 3674

We can also access the information which describes the atoms in contact with the surface topology. In this case two dictionaries are available where the node (surface topology) to atom contacts are stored as key:value data structures. Below are two examples of accessing this data:

>>> atom_contacts = hxacan_002.atom_surface_node_contacts
>>> node_contacts = hxacan_002.surface_node_atom_contacts
>>> print(f"Atoms on the surface: {list(atom_contacts.keys())[:5]}")
Atoms on the surface: [Atom(C1), Atom(C2), Atom(C3), Atom(C4), Atom(C5)]
>>> print(f"Number of Nodes as keys : {len(node_contacts.keys())}")
Number of Nodes as keys : 3674

During the surface calculations a periodic bounding box is used to select atoms which are represented in the slab. This bounding box can be accessed through the .periodic_vectors attributes. These vectors describe the UV (in plane) and W (thickness) vectors of the surface:

>>> hxacan_002.periodic_vectors
[Vector(11.805, 0.000, 0.000), Vector(0.000, 17.164, 0.000), Vector(0.000, 0.000, 7.393)]

We can also retrieve the distance from the origin to the provided reference plane (hkl):

>>> slice_distance = hxacan_002.slicing_plane_distance()
>>> print(f"Slicing Plane Distance : {round(slice_distance, 3)}")
Slicing Plane Distance : 3.696

---

Slip Planes

The class ccdc.particle.SlipPlanes is used to generate slabs of atoms and molecules which represent potential slip planes in a crystal structure. The class also returns various descriptors for these planes. The calculated planes store crystallographic information which describes how the slabs are separated, their thickness, and their positions relative to the unit cell.

Figure 2 illustrates a potential slip plane. In order to compute this, the planes of a crystal object are generated between all the Miller indices between [-9,-9,-9] and [9,9,9]. Two slabs of molecules are then constructed above and below a given plane. If the plane intersects one slab more than the other, the plane is shifted to give a “mid-plane” to ensure the two slabs are evenly divided. The minimum distance between the mid-plane and the atoms in both slabs are calculated, giving in the planar separation as illustrated in Figure 2. By default the tool will present results where the separation_threshold  > 0, however this can be adjusted to study interdigitated systems, where the atoms of the two slabs can interlock.

Figure 6. Slip plane calculation with planar separation.

Note

For more information on the details of the fundamental methodology please see:

“Predicting mechanical properties of crystalline materials through topological analysis”, M. J. Bryant, A. G. P. Maloney, R. A. Sykes, CrystEngComm, 2018,20, 2698-2704, DOI: 10.1039/C8CE00454D.

---

In order to calculate the slip planes we must first create a crystal object and pass it to the SlipPlanes class

>>> from ccdc import io
>>> from ccdc.particle import SlipPlanes
>>> csd = io.EntryReader('CSD')
>>> crystal = csd.crystal("SCCHRN")
>>> planes = SlipPlanes(crystal)

The SlipPlanes class instantiates a list-like object, so the planes variable in this case can be accessed in the same way as any list:

>>> type(planes)
<class 'ccdc.particle.SlipPlanes'>
>>> print(f"Number of slip planes : {len(planes)}")
Number of slip planes : 1

During the calculation the hydrogen bond dimensionality is calculated for the entire crystal. This can be accessed here:

>>> print(f"HB-Dimnensionality : {planes.hbond_dimensionality}D")
HB-Dimnensionality : 0D

As mentioned above, the object is set by default to return all planes where the planar separation is > 0. This can be adjusted using the set_separation_threshold function:

>>> print(f"{len(planes)} slip planes with a separation threshold of {planes.separation_threshold()} A")
1 slip planes with a separation threshold of 0.0 A
>>> planes.set_separation_threshold(-1)
>>> print(f"{len(planes)} slip planes with a separation threshold of {planes.separation_threshold()} A")
7 slip planes with a separation threshold of -1.0 A

It is also possible to convert the object into into a dictionary which contains all the information for each individual plane:

>>> planes.set_separation_threshold(0)
>>> planes_dict = planes.as_dict()
>>> planes_dict
{'slab_separation': [1.095254], 'repeat_distance': [9.284963], 'offset': [0.0], 'orientation': [(1, 0, 0)], 'perpendicular_slip_planes': [[]], 'h_bonded': [False]}

Each plane contains a crystallographic description of its position relative to the unit cell:

>>> plane1 = planes[0]
>>> print(f"Slip plane : {plane1.orientation}")
Slip plane : MillerIndices(1, 0, 0)
>>> print(f"Separation : {round(plane1.slab_separation,3)}A")
Separation : 1.095A
>>> print(f"Repeat distance  : {round(plane1.repeat_distance,3)}A")
Repeat distance  : 9.285A
>>> print(f"Mid plane offset from miller plane : {round(plane1.offset,3)+0}A")
Mid plane offset from miller plane : 0.0A
>>> print(f"Do hydrogen bonds occur across the plane : {plane1.h_bonded}")
Do hydrogen bonds occur across the plane : False
>>> print(f"How many perpendicular planes exist to the slip plane : {len(plane1.perpendicular_slip_planes)}")
How many perpendicular planes exist to the slip plane : 0

We can also investigate the presence of slip planes and overlap of molecules along a specific orientation. This is useful if we are a looking for planes that might have a greater overlap (more negative slab separation) than the limit of -4 Angstrom. Using the existing :object:`ccdc.particle.SlipPlane` that we generated we can specify the orientation we are interested in.

>>> specific_orientation = planes.slip_planes_with_orientation((1,0,0))

This will return a list of SlipPlanes that we can access by iterating over them.

>>> for s_plane in specific_orientation:
...    print(f"Orientation of interest: {s_plane.orientation}")
...    print(f"Separation: {round(s_plane.slab_separation,3)} A.")
...    print(f"Slab_offset: {round(s_plane.offset, 3)+0} A.")
...    print(f"Hbond Present? : {s_plane.h_bonded}")
Orientation of interest: MillerIndices(1, 0, 0)
Separation: 1.095 A.
Slab_offset: 0.0 A.
Hbond Present? : False
Orientation of interest: MillerIndices(1, 0, 0)
Separation: -0.34 A.
Slab_offset: -4.642 A.
Hbond Present? : True
Orientation of interest: MillerIndices(1, 0, 0)
Separation: -4.265 A.
Slab_offset: 2.68 A.
Hbond Present? : True
Orientation of interest: MillerIndices(1, 0, 0)
Separation: -4.265 A.
Slab_offset: -2.68 A.
Hbond Present? : True